Chapter 4: Pricing of Options
An exchange has contracts with multiple strike prices and expires of the same underlying asset. Pricing of Options can be therefore quite challenging. But who decides the premium price when it comes to options contracts:
- Exchanges?
- Regulatory bodies?
The answer lies in understanding the components of option premiums and the factors that affect option pricing.
The regulatory bodies govern exchanges and ensure there’s smooth and fair trade. An exchange is just a platform where buyers and sellers come together to trade.
In fact, price discovery happens when a buyer and a seller execute trades on the exchanges. That forms the basis of asset pricing.
But with options premiums, the pricing mechanism has more layers to it. Since options are a derivative product, the value of options increases or decreases with the change in the underlying asset’s price. That’s not all.
An options value increases or decreases depending on different variables. Each of these variables may have a varied impact while the impact itsel will differ as per the type of contract.
Before getting into which factors affect the option premiums, let’s learn how option premiums are priced.
Concepts of Option Premiums
There are few mathematical models that can be used to derive the value of option premiums. Based on these models, option premium pricing can be determined on approximation, although markets are dynamic and prices may vary in practice when compared with theoretical models.
To simplify things, let’s explore the following concepts:
- Intrinsic Value and Time Value
- Moneyness of Option Premiums
- Intrinsic Value and Time Value
Option premiums comprise of 2 components:
- Intrinsic Value
- Time Value
That’s why…
Formula of Options Premium
Option Premium = Intrinsic Value + Time Value (Extrinsic Value)
The Intrinsic Value reflects the amount by which the option is “In The Money”, meaning if the right is exercised today, the option would be profitable.
The Time Value reflects the time remaining until the option expires and the expected volatility of the underlying asset.
Intrinsic value for Call and Put options are calculated as follows:
Formula of Intrinsic Value (Call Options)
Intrinsic value = Strike Price – Spot Price
Formula of Intrinsic Value (Put Options)
Intrinsic value = Spot Price – Strike Price
Please note that Intrinsic Value cannot be negative.
This is because options contracts give the buyer a choice to exercise or not exercise the contract. A trader will exercise the option only when it is profitable to the buyer.
If the buyer is incurring a loss, he would allow the options to expire worthless and lose the premium paid for buying the option. But, he wouldn’t lose any more money than the premium paid at the time of buying the contract.
Let’s take a practical example to understand the concept of Intrinsic Value by adding one more concept of the Moneyness of Option Premiums.
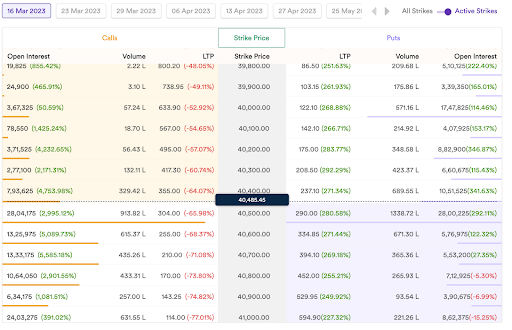
The above image is an Option Chain, a visual representation of strike prices and their LTP (Last Traded Prices).
The left side of the option chain has call option premiums, and the right-hand side put option premiums. All the strike prices are in ascending to descending order and the Spot Price is highlighted at the centre.
The spot price of Bank Nifty is 40,500 (rounded off in the image above). Now to the concept of the Moneyness of option premiums.
Moneyness of Option Premiums
Moneyness is the representation of the interplay between an option’s Strike Price and Current Market Price of the underyling.
An option’s moneyness determines whether an option contract is At The Money (ATM), Out of The Money (OTM), or In The Money (ITM).
You will hear this jargon a lot while trading options so here’s what they mean.
- An option is said to be “At The Money” (ATM) when the price of an underlying asset is equal to the strike price of the option contract.
- An option is “Out of The Money” (OTM) when the options strike price far away from the price of the underlying asset.
- An option is said to be “In The Money” (ITM) if the option buyer can make profits by exercising the option today.
A few things to note here are as follows:
- ITM has higher values since it has some Intrinsic Value.
- ATM and OTM options have zero Intrinsic Value since we know that Intrinsic Value cannot be negative.
- As time passes by, options lose the Time Value component.
Let’s refer to the option chain again and take examples to simplify the concept of Intrinsic & Time value and the relation of option premiums relative to their moneyness.
Example:
40500 Call and Put Options are At the Money currently since the Spot Price = Strike Price.

But ITM and OTM will differ for call and Put options.
For Call Options:
All the Strikes that are above 40500 (less Than 40500) in the option chain are In the Money and those below 40500 ( greater than 40500) are Out of the Money Options.

(shaded area on the image represents ITM)
For Put Options:
All the Strikes that are below 40500 (less Than 40500) in the option chain are are Out of the Money Options. And and those above 40500 ( greater than 40500) In the Money Put Options.

(shaded area on the image represents ITM)
Did you notice, ITM call options have more value than ATM or OTM Calls?

The reason is, ITM Call Options have Intrinsic Value + Time Value
For example, the Spot is currently 40500 so an ITM Call option of 40000 Calls is trading at Rs. 633 (refer to the image).
As we discussed, the option premium has 2 components Intrinsic Value + Time Value
Option premium = Intrinsic Value + Time Value ( Extrinsic Value )
Calculation of Option Premium
40000 Call Option = IV of 500
IV = Spot 40500 – Strike 40000 + Time Value of 133
Time Value = Option Premium 633 – IV 500 = 133
While an ATM option may have some Time Value depending on the spot price, OTM options only have the Time Value component in the option premium price.
Every options trader should know that as time passes, the Time Value component (Extrinsic Value) decreases from the option premium and the depreciation in premiums is much faster when the option contracts are nearing their expiry.
This decreasing Time Value has a name: Theta Decay (Time Decay). It acts as an unseen edge for option sellers.
But you may ask, why is this concept so important?
It’s because the moneyness of an option contract affects the pricing of options premiums and the probability that it will expire in the money.
Options that are ITM tend to have higher values since they have a higher probability of expiring in favour of the buyer, while options that are OTM tend to have lower values as they have a lower probability of expiring in the money.
For option sellers, OTM option selling can thus be a profitable strategy. There is a caveat though. It can be profitable only for those who understand the concept of time decay relative to the moneyness of options.
The reason option sellers are able to make consistent profits is that OTM options have a lesser probability of expiring in favour of the buyer.
Moreover, it’s likely that the option buyer will not exercise the right to buy the underlying asset if the trade isn’t profitable, just as we saw in our example, in Mr Bull’s case.
Thus, the premiums which buyers pay to sellers, lose their entire value and go down to zero, at expiry, when buyers choose not to exercise the options.
Time to expiry is fixed since it’s mentioned in the options contract and with each day that passes by, option premiums lose some Time Value component, the decay is much faster in OTM strikes and this acts as an unseen edge that is available to option writers that help them to increase their probability to make consistent profits.
The Moneyness of options also helps option sellers in risk management. Sellers get ample time to react if they sell OTM options and they can do certain adjustments to manage their risk.
So traders, based on the above facts, we can establish that, if an option seller who has good risk management skills, can consider option selling as a good business opportunity, to generate some really good ROIs on the capital deployed.
Option Premium Pricing Models
Theoretically, there are mathematical models that can be used to determine the approximate optimum pricing of option premiums.
The reason we should consider these models in the approximation is that these models don’t account for abnormal moves or unforeseen fluctuations in the markets that can cause higher volatility.
However, these models can be used for traders, especially traders who speculate in the options market , for better decision-making.
In this Chapter, we shall learn about 2 popular and widely used trading modules to arrive at the right value of option premiums.
- The Binomial Pricing Model
- The Black and Scholes Model
The Binomial Pricing Model
Developed in 1978 by William Sharpe, the Binomial option pricing model has proven to be one of the most flexible and popular approaches to valuing option premiums.
The Binomial Pricing Model represents the potential prices of an option’s underlying asset using a tree-like structure. It assumes that time is divided into discrete and equally spaced intervals.
At each interval, the asset’s price can either move up or down by fixed rates. These movements are determined by simulated probabilities based on factors like volatility and time.
Here’s the catch. The Binomial Pricing Model is known to be quite cumbersome as various probabilities are simulated. At the same time, the model is pretty accurate and thus works best for long-dated maturity options.
It’s been widely used since it is able to handle a variety of conditions for which other models cannot easily be applied.
Since the Binomial Pricing Model is based on the interpretation of an underlying instrument over a period of time rather than a single point, it is used to value American-style options that are exercisable at any time as well as Bermudan options that are exercisable at specific instances of time.
Definition of Bermudan Options
Bermudan options can be exercised at specific dates before expiration, whereas American options can be exercised at any time before expiration, and European options can only be exercised at expiration.
Black and Scholes Model
The Black and Scholes Model was published in the year 1973 by Fisher Black and Myran Scholes. Its one of the most widely used mathematical models and ever since the model was published, it led to a boom in options trading.
The model has been credited with providing mathematical logic to the activities of options markets across the globe.
This model is used to calculate the theoretical price of options with assumptions such as (but not limited to):
- Ignoring the dividend paid during the life of the option contract
- No arbitrage opportunities available
- Market movements are random – it’s difficult to predict the market direction at all times
While also using key fundamental factors of option premiums that are the price of the stock, strike price, volatility, time to expiry, and short term risk-free interest rates.
The Black–Scholes model assumes that the market consists of at least one risky asset, usually known as stock, and one riskless asset, usually called the money market, cash, or bond.
The standard Black and Scholes Model is only used to price European options, as it does not take into account that American options could be exercised before the expiration date.
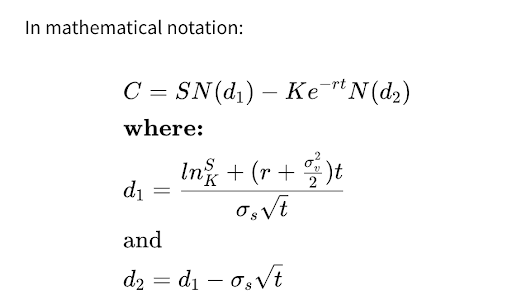
where,
C= Call option price
S= Current stock (or other underlying) price
K= Strike price
r= Risk-free interest rate
t= Time to maturity
N= A normal distribution
Although options traders have access to a variety of online options calculators, and many of today’s trading platforms have robust options analysis tools, including indicators that perform the calculations and display the options pricing values almost instantly, the Black and Scholes Model has been the most widely accepted model across the world.
In Fact, options markets in the Indian exchanges follow the Black and Scholes model to determine the pricing of options contracts.
So these were some of the option premium pricing models that are used to determine option premium pricing. The idea behind these mathematical models is to derive a fair value for option premiums and now let’s discuss the factors that affect the movements of option premium prices.
Factors Affecting the Pricing of Option Premiums
Pricing of the option premiums depends on a lot of factors such as what is the spot price of the underlying asset currently traded, strike prices of options, time to expiry, volatility in the underlying asset and the current interest rates in the economy.
These are fundamental parameters for option premium pricing. To further understand how options are priced and the impact of variable factors on option premiums, let’s decode these variables and how these factors determine and affect option premium prices. Don’t worry, we shall keep things super simple.
1. Current Market Price Or Spot Price
With every increase or decrease in the value of the underlying asset, the option prices keep on changing.
If the price increases, call option prices go up whereas put option prices decrease.
If the price of the underlying asset decreases, the value of put options increases while the value of the call option decreases.
2. Time to Expiry of the Contract
Options contracts expire post the last day of the contract period. Option premiums also include some additional pricing if the time to expire is in the future.
The longer the maturity of option premiums greater the uncertainty and therefore higher the premiums.
As we saw that options premiums have intrinsic and Time Value in their pricing, the Time Value component is maximum at the starting date of the contract and as time passes by the Time Value component decreases and goes down the zero at the expiry.
3. Volatility of Underlying Asset
Volatility refers to the magnitude of movement in the underlying asset price up or down from the current market price and it affects the option premiums of both call and put options in the same way.
The higher the volatility, the higher would be the option premium prices since there is a high risk for the buyer of the option of options going out of the money and option sellers fear option prices going against them.
4. Interest Rates
Interest rate has an inverse impact on option premium prices. Interest rates affect different options differently.
Most times, an increase in interest rates will cause an increase in the call premiums and cause put premiums to decrease.
Unlike other option Greeks (which we shall discuss in the coming Chapters), which are dynamic and affect the option prices on a relatively regular basis, the impact of interest rates on option premiums is barely noticeable but indeed important.